こんにちは!
今日はカルノーサイクルがどんなものかをグラフとともになるべくわかりやすく説明してみます。
今回の内容を基礎として次回は考察をしていくため、イメージをしっかりつかめたらうれしいです!(^^)!
ではやっていきます
カルノー・サイクルとは何か
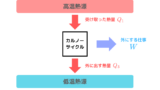
カルノーサイクルとは高温熱源と低温熱源を結び付け、外に仕事を取り出すことが可能な可逆可能サイクルです。
といわれてもピンとこないですよね(^▽^;)
なのでグラフを使って説明します。
カルノーサイクルはおもに等温変化と断熱変化から構成される1サイクルです。
pv図を書くと
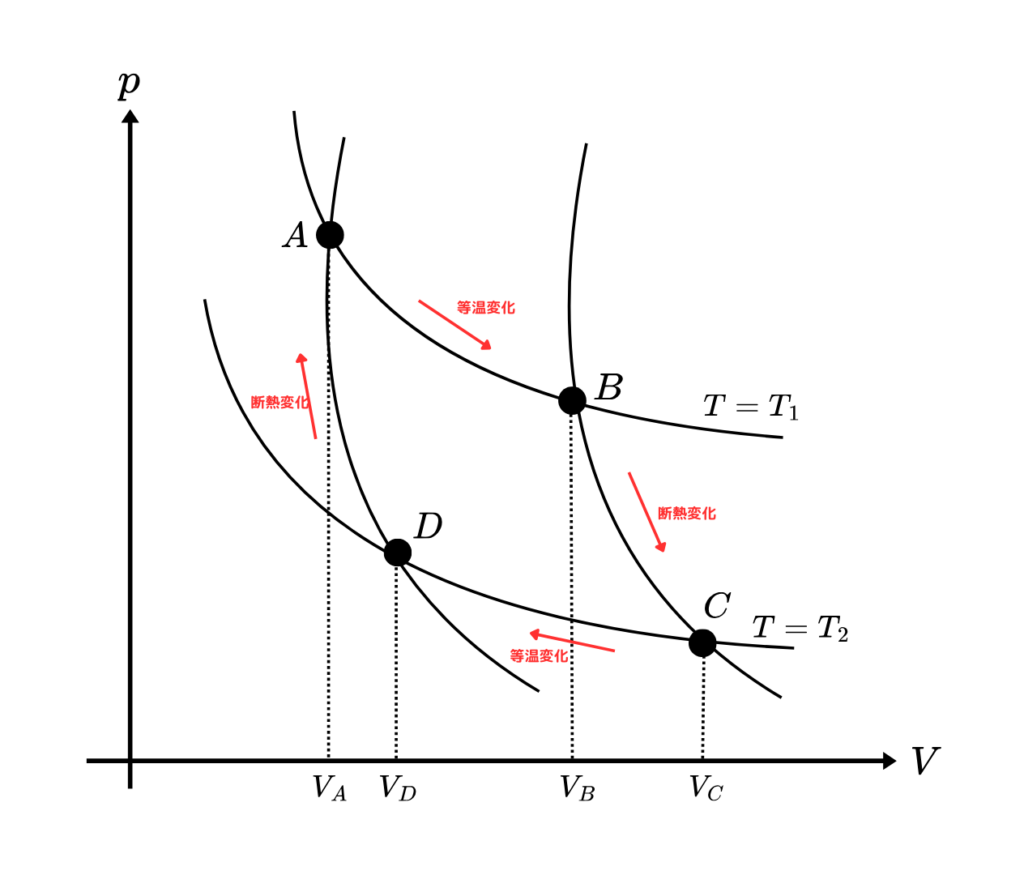
このような図になります。
等温変化と等圧変化のみで循環しているのがわかりますね。
ではこの4つの過程それぞれにおける仕事と熱量を求めてみたいと思います。
作業物質は\( n \) [mol] です。
(1)等温膨張 : A → B
まずは外にする仕事 \( W_{1} \) です。
$$ \begin{eqnarray}
W_{1} &=& \int_{A \rightarrow B} p dV \\[7pt]
&=& nRT_{1} \int_{V_{A}}^{V_{B}} \frac{1}{V} dV \\[7 pt]
&=& nRT_{1} \log \frac{V_{B}}{V_{A}}
\end{eqnarray} $$
つぎに熱量です。
等温変化であることから内部エネルギーは変化しません。
これより、外にする仕事と高温熱源から受け取る熱量は同じなので
$$ Q_{1} = W_{1} = nRT_{1} \log \frac{V_{B}}{V_{A}} $$

(2)断熱膨張 : B → C
外にする仕事 \( W_{2} \) は
$$ W_{2} = \int_{B \rightarrow C} p dV $$
ここでポアソンの法則 \( pV^{\gamma} = k’ \) より、
$$ \begin{eqnarray}
W_{2} &=& \int_{V_{B}}^{V_{C}} \frac{k’}{V^{\gamma}} dV \\[7 pt]
&=& \frac{k’}{1- \gamma}[V^{1- \gamma}]_{V_{B}}^{V_{C}} \\[7 pt]
&=& \frac{k’}{\gamma \ – 1}[V_{B}^{1- \gamma} – V_{C}^{1- \gamma}] \\[7 pt]
\end{eqnarray} $$
ポアソンの法則より、 \( k’ = p_{B}V_{B} = p_{C}V_{C} \) なので、
$$ \begin{eqnarray}
\qquad &=& \frac{1}{\gamma \ – 1}(p_{B}V_{B}-p_{C}V_{C}) \\[7 pt]
&=& \frac{nR}{\gamma \ – 1}(T_{1}-T_{2}) \\[7 pt]
\end{eqnarray} $$
マイヤーの関係式 \( C_{p}-C_{V}=nR \) とポアソンの法則導出の際の変換式 \( \gamma = \frac{C_{p}}{C_{V}} \) を用いると、
$$ W_{2} = C_{V}(T_{1}-T_{2}) $$
このようにして外にする仕事が求まりました!
熱量 \( Q_{2} \) に関しては断熱変化なので熱の出入りはなく、
$$ Q_{2} = 0 $$
となります。

マイヤーの関係式とポアソンの法則の導出についてはこちらをご覧ください↓↓↓
(3)等温圧縮 : C → D
等温膨張 (A → B) の時と同様に求めます。
まず外にする仕事 \( W_{3} \) は
$$ \begin{eqnarray}
W_{3} &=& \int_{C \rightarrow D} p dV \\[7 pt]
&=& nRT_{2} \int_{V_{C}}^{V_{D}} \frac{1}{V} dV \\[7 pt]
&=& nRT_{2} \log \frac{V_{D}}{V_{C}} \\[7 pt]
\end{eqnarray} $$
となります。ここで、 \( V_{D} \lt V_{C} \) なので、 \( \log \frac{V_{D}}{V_{C}} \lt 0 \) です。
つまり、 \( W_{3} \lt 0 \) なので、この仕事は外からされた仕事なのです。
低温熱源に出す熱量は、内部エネルギーの変化がないことから
$$ Q_{3} = -nRT_{2} \log \frac{V_{D}}{V_{C}} $$
です。

(4)断熱圧縮 : D → A
断熱膨張 (C → D) の時と同様に考えます。まず外にする仕事 \( W_{4} \) は
$$ \begin{eqnarray}
W_{4} &=& \int_{D \rightarrow A} p dV \\[7 pt]
&=& k’ \int_{V_{D}}^{V_{A}} V^{-\gamma} dV \\[7 pt]
&=& \frac{k’}{\gamma \ – 1}[V_{D}^{1- \gamma}-V_{A}^{1-\gamma}] \\[7 pt]
&=& \frac{1}{ \gamma \ – 1}(P_{D}V_{D}-P_{A}V_{A}) \\[7 pt]
&=& \frac{nR}{\gamma \ – 1}(T_{2}-T_{1}) \\[7 pt]
&=& C_{V}(T_{2}-T_{1}) \\[7 pt]
\end{eqnarray} $$
となります。
ここで、 \( T_{2} \lt T_{1} \) より、 \( W_{4} \lt 0 \) です。
つまりこの仕事は外からされた仕事なのです。
わかりやすく
$$ W_{4} = -C_{V}(T_{1}-T_{2}) $$
と書き換えておきます。
そして断熱変化より熱量の出入りはないので
$$ Q_{4} = 0 $$
です。

まとめ
本日のまとめです。
まずカルノーサイクルとは
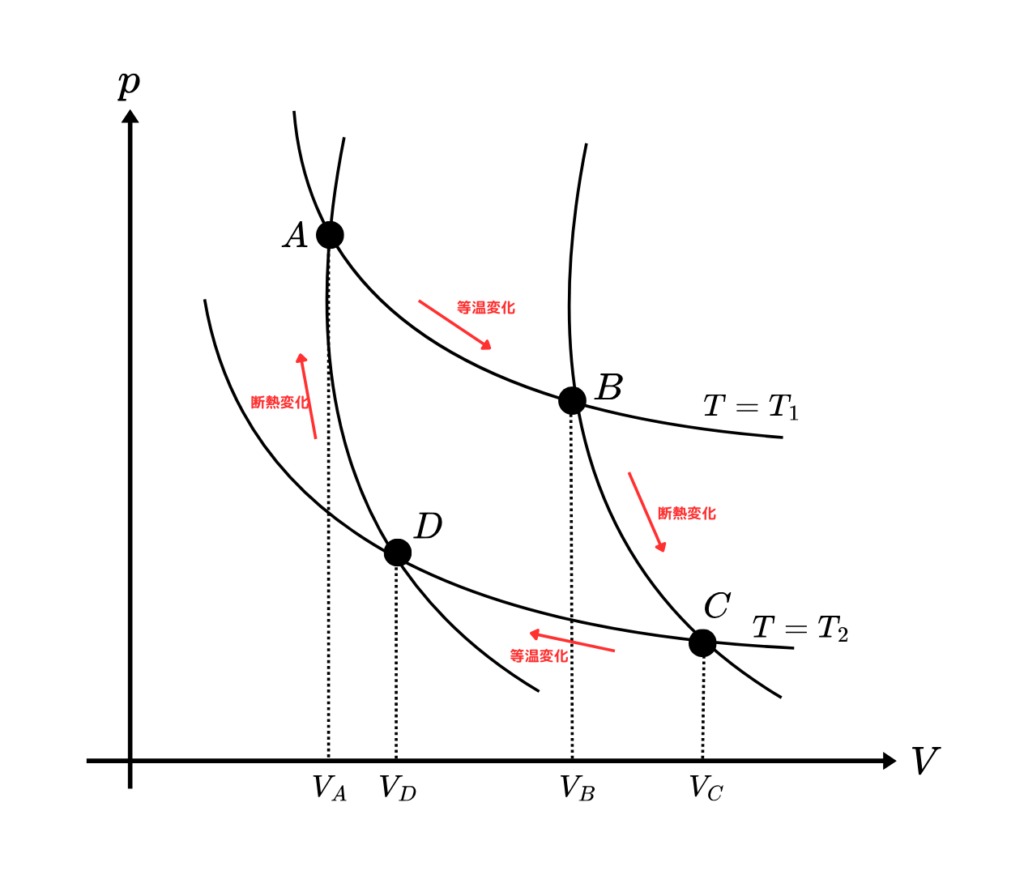
このようなpV図を描きます。そしてそれぞれの仕事と熱量は

このようになります。
次回はこれを用いてカルノーサイクルの熱効率を求めていきたいと思います!(^^)!
ではまた(^^)/~~~
次回の熱効率の記事です↓↓↓