こんにちは!
今日は主にいろいろな熱力学過程で生じるエネルギーについてそれぞれ定義していきたいと思います
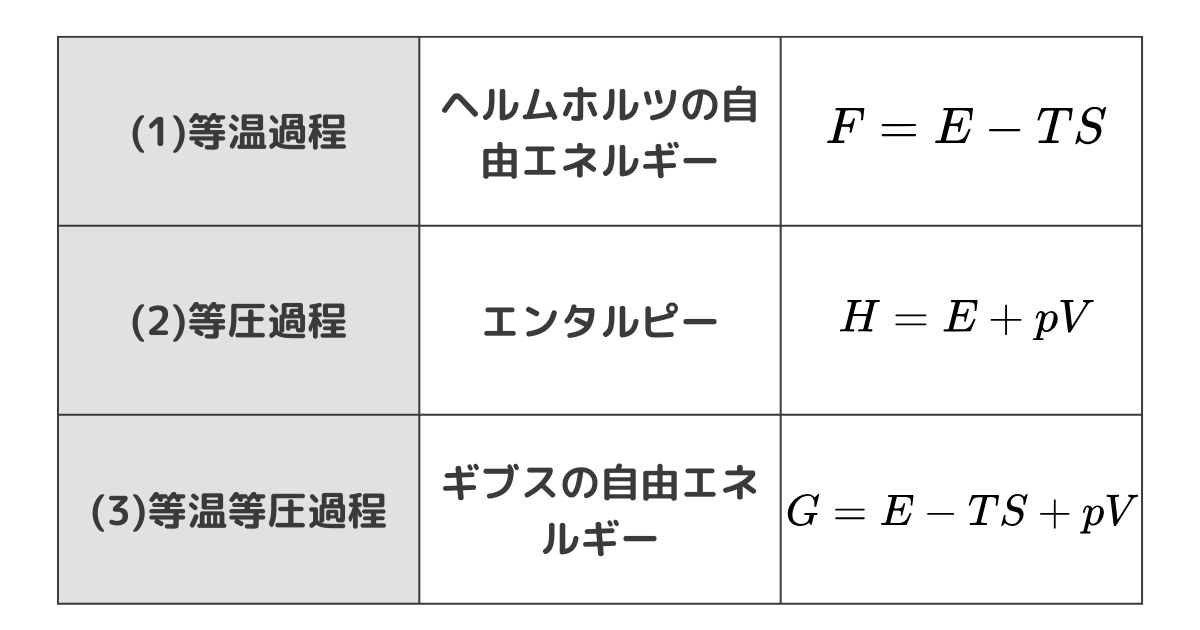
主にヘルムホルツの自由エネルギー・エンタルピー・ギブスの自由エネルギーを扱っていきます
ではやっていきましょう!
準備としての熱力学第1法則
内部エネルギーを状態量のみの式で表してみます。
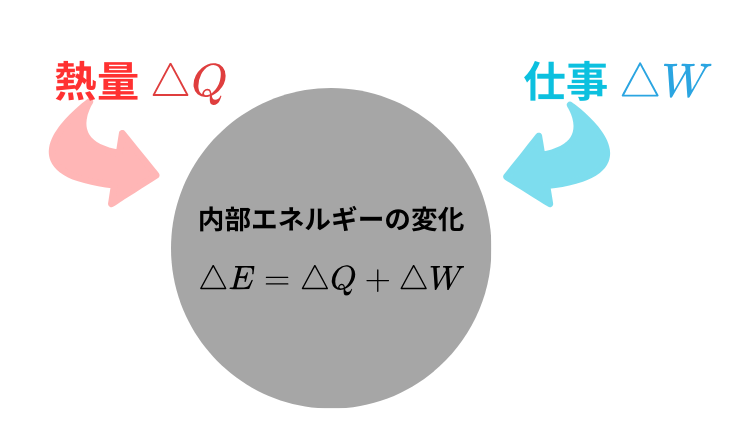
まずは熱力学第1法則を思い出しましょう。
熱量 \( \delta Q \) を受け取り、\( \delta W \) の仕事をされるとき、内部エネルギーの増加は
$$ dE = \delta Q + \delta W $$
と表されます。
そしてこれらの微小な熱量、仕事はそれぞれ
$$ \delta Q = T dS $$
$$ \delta W = -pdV $$
と表すことが出来るのです。
\( S \) はエントロピーです。これについては以下の記事で述べているので心配な方はどうぞ↓↓↓
これら3つの式を用いると微小な内部エネルギーの変化は
$$ dE = TdS – pdV \quad (1) $$
と書き表すことが出来ます。
この(1)式は状態量のみ式になっています!
この式を用いてこれからの話を進めていきます。
おもに等温過程・等圧過程・等温等圧過程のエネルギーについて考えます

等温過程:ヘルムホルツの自由エネルギー
ではまず等温過程のときの物質が外にする仕事について考えてみましょう。
外にする微小な仕事量 \( \delta W \) は(1)式を用いると
$$ \begin{eqnarray}
\delta W &=& pdV \\[7pt]
&=& -dE+TdS \\[7pt]
&=& -d(E – TS) \\[7pt]
\end{eqnarray} $$
ここで今回は等温変化なので \( T \) が一定のためすべて \( d \) でまとめることができました。
この \( E-TS \) の部分を文字でおいてみると、
$$ F = E -TS $$
となり、これがヘルムホルツの自由エネルギーです。
外にする微小な仕事量は
$$ \delta W = -dF $$
とあらわされ、ホルムヘルツの自由エネルギーの変化によって仕事をするといえるのです。
また、等温過程において外への仕事に使えるエネルギーは内部エネルギー \( E \) から無秩序な熱エネルギー \( TS \) を引いたものであるといえます。

等圧過程:エンタルピー
次は等圧過程のエネルギーについて考えていきます。
次は外にする仕事量ではなく、受け取った微小な熱量 \( \delta Q \) について考えます。
先ほどと同じように(1)式を使って、
$$ \begin{eqnarray}
\delta Q &=& TdS \\[7pt]
&=& dE +pdV \\[7pt]
&=& d(E+pV) \\[7pt]
\end{eqnarray} $$
となります。
今回は等圧過程により、 \( p \) は一定なので \( d \) にまとめることが出来ました。
この \( E + pV \) の部分を文字で置くと、
$$ H = E+pV $$
となり、これをエンタルピーと呼びます。
(エントロピー \( S \) と名前が似ていて混ざりやすいので気を付けましょう^^;)
受け取った微小な熱量は
$$ \delta Q = dH $$
と表すことができ、受け取る熱量はエンタルピーの変化に依存していることがわかります。
また、等圧過程において受け取る熱量は内部エネルギー \( E \) と \( pV \) の総和であることがわかります。

等温等圧過程:ギブスの自由エネルギー
最後に等温等圧過程について考えます。
等温等圧過程において、\( T \) と \( p \) は一定なため、系の状態はただひとつに決まってしまいます。( \( V \) が決まってしまうため)
なので今回は粒子の出入りを許すとして、\( N \) も状態変数だと考えてみます。
系に粒子1個を加えるために必要なエネルギーを化学エネルギーといい、 \( \mu \) で表すことが出来ます。
これにより粒子数が \( dN \) だけ増加すると内部エネルギーは \( \mu dN \) だけ増加するということができます。
これを考慮すると(1)式は少し変更を加える必要があり、
$$ dE = TdS – pdV + \mu dN \quad (2) $$
となります。
粒子数 \( dN \) を系から追加するためには外からの仕事は \( \mu dN \) だけ必要なので、逆に粒子数 \( dN \) を放出するには外に \( -\mu dN \) だけ仕事をすればいいわけです。
これを \( \delta W’ \) と表すと、(2)式を用いて
$$ \begin{eqnarray}
\delta W’ &=& -\mu dN \\[7 pt]
&=& -dE + T dS – pdV \\[7pt]
&=& -d(E – TS + pV) \\[7pt]
\end {eqnarray} $$
となります。
等温等圧過程より、 \( T \) 、\( p \) を一定なので \( d \) でまとめることが出来ました。
この \( E -TS+pV \) の部分を文字で置いて
$$ G=E-TS+pV $$
これをギブスの自由エネルギーといいます。
等温等圧過程では、系が外にする仕事は
$$ \delta W’ = -dG $$
とあらわされ、ギブスの自由エネルギーの変化量に依存するといえます。

まとめ
いかがでしたか(*^^*)
本日のまとめです。
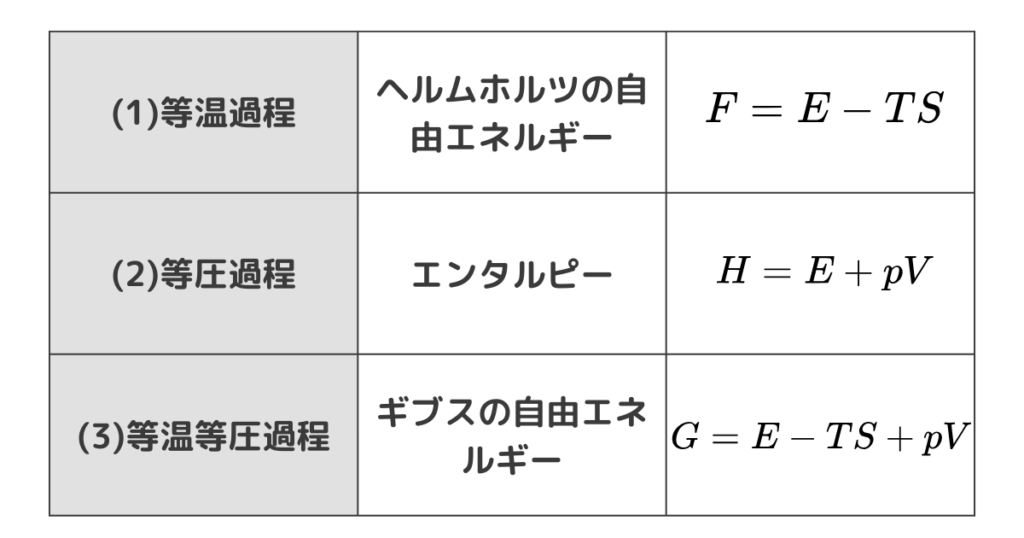
ホルムヘルツの自由エネルギー、エンタルピー、ギブスの自由エネルギーそれぞれどんなものか整理して、それぞれの過程におけるエネルギーの流れを掴んでおきましょう。
ではまた(^^)/~~~