こんにちは(*^^)v
今回は前回求めたカルノーサイクルの熱量、仕事を使って熱効率を求めてみたいとおもいます!
カルノーサイクルそれぞれの熱量、仕事の導出方法はこちらをご覧ください↓↓↓
ではやっていきましょう!
準備
以下のカルノーサイクルについて考えていきます。
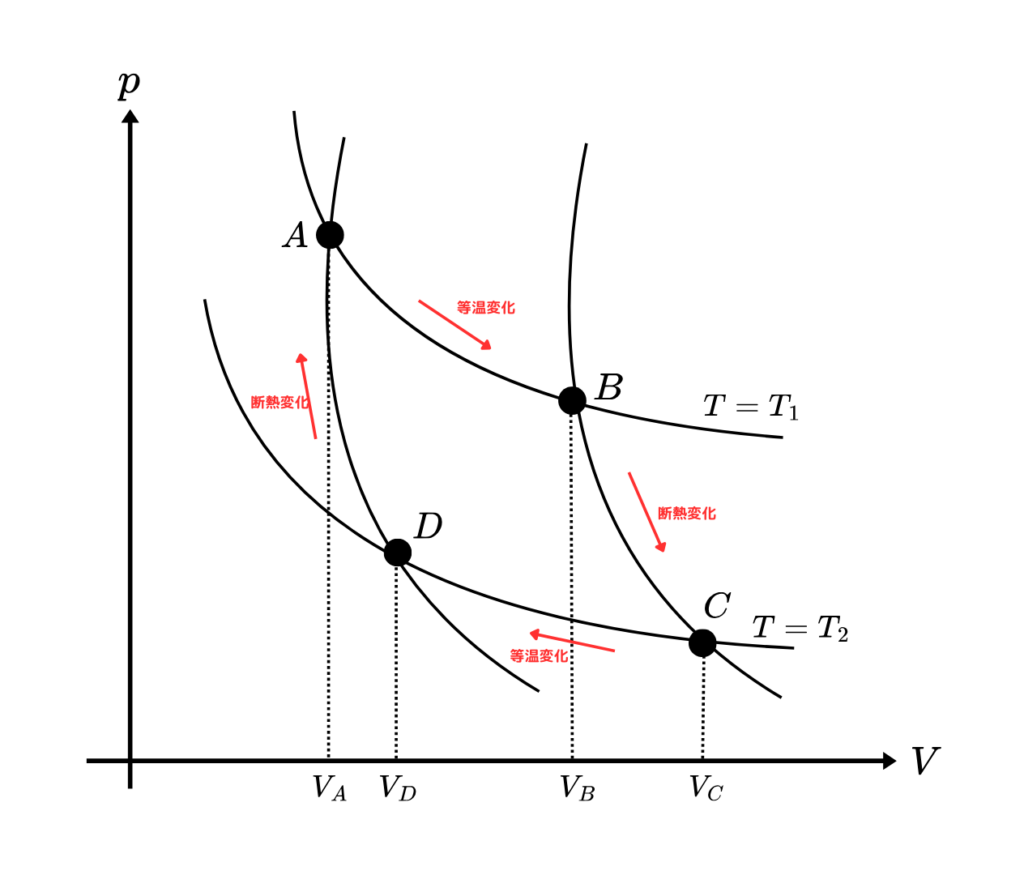
そしてこれは前回の記事のまとめになりますが、それぞれの過程における仕事と熱量はこのようになります。

熱効率とは熱機関が受け取った熱量のうちどのくらいを仕事に使ったかをしめす割合です。
取り入れた熱量を \( Q \) 、外にする仕事を \( W \) とすると熱効率 \( e \) は
$$ e = \frac{W}{Q} $$
と表すことが出来ます。
つまりカルノーサイクルの外にする仕事の量と受けった熱量の値がわかれば熱効率が求められるというわけです。
カルノーサイクルの外にする仕事の量
外にする仕事の量は
$$ W=W_{1}+W_{2}+W_{3}+W_{4} $$
で求まります。
それぞれ値を代入すると
$$ \begin{eqnarray}
W &=& nRT_{1}\log \frac{V_{B}}{V_{A}} + C_{V}(T_{1}-T_{2})+nRT_{2}\log \frac{V_{D}}{V_{C}} – C_{V}(T_{1}-T_{2}) \\[7 pt]
&=& nRT_{1} \log \frac{V_{B}}{V_{A}} – nRT_{2} \log \frac{V_{D}}{V_{C}} \\[7 pt]
\end{eqnarray} $$
ここでポアソンの法則より
$$ T_{1}V_{B}^{\gamma – 1} = T_{2}V_{C}^{\gamma – 1} $$
$$ T_{1}V_{A}^{\gamma – 1} = T_{2}V_{D}^{\gamma – 1} $$
この2式が成り立つ。
これらを組み合わせて、 \( T_{1},T_{2} \) を消すと、
$$ \left(\frac{V_{D}}{V_{A}} \right)^{\gamma – 1}=\left(\frac{V_{C}}{V_{B}}\right)^{\gamma – 1} $$
これを整理して、
$$ \frac{V_{B}}{V_{A}} = \frac{V_{C}}{V_{D}} $$
という式が出来ます。
これを先ほどの仕事の値に代入すると、
$$ W=nR(T_{1}-T_{2})\log \frac{V_{B}}{V_{A}} $$
となります。

カルノーサイクルの受け取った熱量の値
\( Q_{1}\) は受け取る熱量、 \( Q_{3}\) は出す熱量です。
熱効率をもとめるには受け取った熱量の値がわかればいいので、今回は \( Q_{1} \) の値を使います。
$$ Q=nRT_{1} \log \frac{V_{B}}{V_{A}} $$
となります。

熱効率を求める
では熱効率を求めてみましょう。
$$ \begin{eqnarray}
e &=& \frac{W}{Q} \\[7pt]
&=& \frac{nR(T_{1}-T_{2})\log \frac{V_{B}}{V_{A}}}{nRT_{1} \log \frac{V_{B}}{V_{A}}} \\[7 pt]
&=& 1-\frac{T_{2}}{T_{1}} \\[7pt]
\end{eqnarray} $$
となりました!
熱効率が求められましたね!(^^)!

カルノー機関のざっくりとしたイメージ
最後にカルノーサイクルのざっくりとしたイメージ、仕事や熱量の流れを図にしてイメージを掴んでもらいます。
カルノーサイクルは高温熱源から熱量 \( Q_{1} \) を受け取り、そのうち \( W \) だけ外に仕事をし、低温熱源に向かって \( Q_{3} \) だけ熱量を出しています。
図にすると、
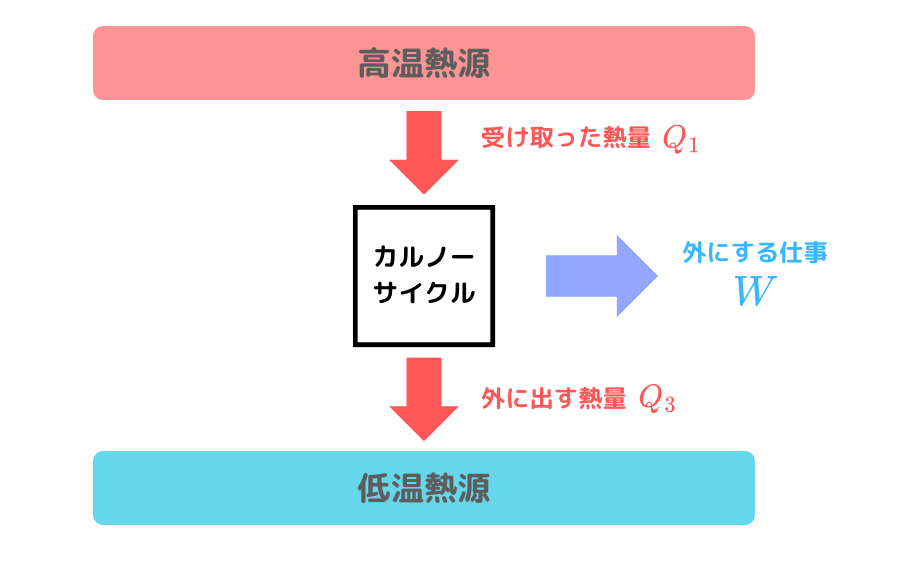
こんなかんじです。
熱効率とはこの図における受け取った熱量からどれだけのぶんを仕事に変換できたかを示す値でした。
図でイメージを掴んだ方がわかりやすいですね(*^^)v
まとめ
今回はカルノーサイクルにおける熱効率を求めました。
熱効率がどんなものであるかと、カルノーサイクルの仕事と熱の流れをおさえられたらうれしいです!
ではまた(^^)/~~~



