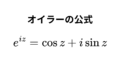こんにちは!
今回は複素対数関数の実部と虚部を考えてみたいと思います。
この記事でわかること
複素対数関数の実部と虚部
$$ \log z = \log |z| + i (\arg z +2n \pi ) $$
の導出とそれを用いた具体的な計算
それではやっていきましょう!
log z の実部と虚部の導出
\( y= \log z \) の実部と虚部が知りたいのでこれを文字で置きます。
つまり、
$$ y= \log z = a + ib $$
と置きます。
今回の問題ではこの 実部\( a \) と 虚部\( b \) の値を求められればOKというわけです。
この式を少し変形しましょう。
$$ z=e^{y}=e^{a+ib} = e^{a}(\cos b + i\sin b) \quad \cdots (1) $$
最後の変形はオイラーの公式を使いました。
また、もう一度オイラーの公式を使って別の式を作ります。
$$ z=re^{i \theta} = r (\cos \theta + i \sin \theta) \quad \cdots (2) $$
ここで \( r \) は \( z \) の絶対値、 \( \theta \) は偏角です。
(1)式と(2)式を比較してみましょう。すると、
$$ r=e^{a} \Leftrightarrow a=\log r $$
$$ b=\theta + 2n\pi $$
となり実部 \( a \) と虚部 \( b \) が求まりました!( \( n \) は整数です。)
\( r \) は \( z \) の絶対値、 \( \theta \) は偏角なので、
$$ \begin{eqnarray}
log z &=& \log r +i( \theta + 2n\pi ) \\[7pt]
&=& \log |z| + i( \arg z + 2n \pi ) \\[7pt]
\end{eqnarray} $$
これにて導出が終了しました!

具体例 : \( i^{\frac{1}{4}} \) の取る値
では、これを使った具体例として
$$ i^{\frac{1}{4}} $$
のとる値について考えてみましょう。
まずは少しこれを変形します。
$$ i^{\frac{1}{4}} = e^{\frac{1}{4} \log i} $$
ここで \( \log i \) の部分を先ほど導出した式を用いて実部と虚部に分けてみましょう
$$ \begin{eqnarray}
\log i &=& \log |1| + i( \frac{ \pi }{2} + 2n \pi ) \\[7pt]
&=& i( \frac{ \pi }{2} + 2n \pi ) \\[7pt]
\end{eqnarray} $$
となるので、
$$ \begin{eqnarray}
i^{\frac{1}{4}} &=& e^{\frac{1}{4} \log i} \\[7pt]
&=& e^{\frac{1}{4} i( \frac{ \pi }{2} + 2n \pi )} \\[7pt]
&=& e^{i( \frac{ \pi }{8} + \frac{1}{2} n\pi )} \\[7pt]
\end{eqnarray} $$
となります!
最後に \( n \) を場合分けしましょう
\begin{eqnarray}
i^{ \frac{1}{4} }
\begin{cases}
e^{i \frac{ \pi }{8}} & (n=2m) \\[7pt]
e^{i \frac{5}{8} \pi} & (n=2m+1) \\[7pt]
\end{cases}
\end{eqnarray}
ちなみに、この \( i^{\frac{1}{4} } \) のように2つ以上の値を取るものを多価関数といいます。
まとめ
いかがだったでしょうか!
複素対数関数の実部と虚部の求め方が理解出来たらうれしいです。
次回はこれを使って多価関数とリーマン面について説明していきます(*^^*)
ではまた(^^)/~~~