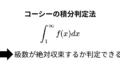こんにちは!
今回は収束半径と収束円の意味と求め方について扱っていきます。
それではやっていきましょう!
べき級数の簡単な説明
まずはべき級数の簡単な説明をしたいと思います。
いま、無限級数
$$ P(z)=a_{0}+a_{1}z+a_{2}z^2+ \cdots = \displaystyle \sum_{n=0}^{\infty}a_{n}z^n $$
があったとき、この形の級数をべき級数(power series)といいます。
今回はこのべき級数の性質を扱っていきます。
収束円・収束半径とは
さきほどの話の続きですが、上のべき級数の式を見てもらうとわかる通り、べき級数には次のいずれかひとつが成立します。
(1)すべての \( z \) に対して絶対収束
(2)\( R \gt 0 \) となる \( R \) があるとき、 \( R \lt |z| \) で絶対収束、 \( R \gt |z| \) で発散
(3)0以外のすべての \( z \) に対して発散
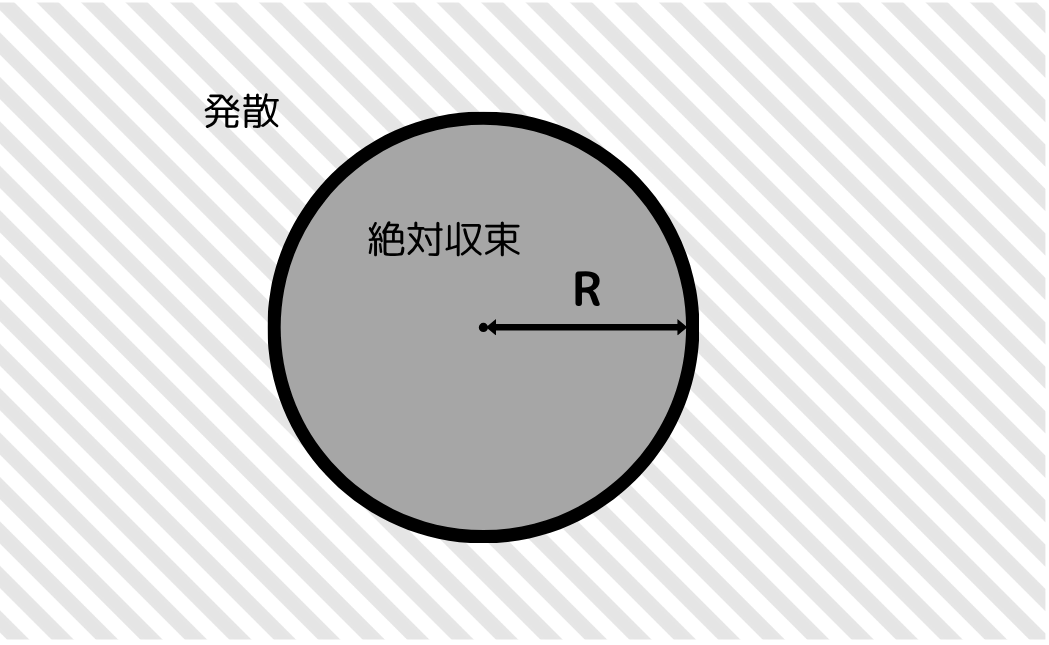
この(1)~(3)をまとめてイメージ図で表してみます。
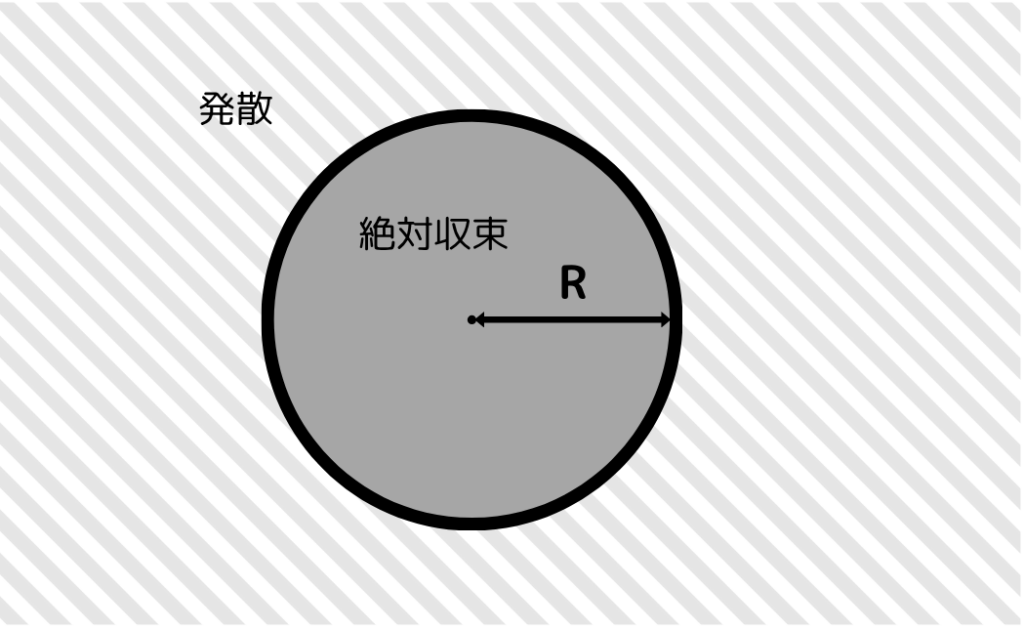
こんなかんじです。
このようにそれぞれの級数はそれぞれ特有の円を持っています。
この円を収束円(circle of convergence)といい、\( R \) を収束半径(radius of convergence)といいます。
収束半径の求め方
基本的な収束半径の求め方はおもに2つあります。
①ダランベールの判定法を用いた公式(係数比判定法)
②コーシーアダマールの公式
今回はこれらを紹介していきます。
ダランベールの判定法を用いた公式(係数比判定法)
あるべき級数 \(\displaystyle \sum_{n=0}^{\infty}a_{n}z^n\) の収束半径 \( R \) は
$$ R= \displaystyle \lim_{n \to \infty} \frac{|a_{n}|}{|a_{n+1}|} $$
で求められる
この定理はダランベールの収束判定法から導き出すことが出来ます。
では導出してみます。
[導出]
ダランベールの収束判定法より、べき級数が絶対収束するとき
$$ \displaystyle \lim_{n \to \infty} \left| \frac{a_{n+1}z^{n+1}}{a_{n}z^n} \right| \lt 1 $$
が成立するはずです。
この式を変形して、
$$ |z| \lt \displaystyle \lim_{n \to \infty} \frac{|a_{n}|}{|a_{n+1}|} $$
となり、\( z ) がこの範囲を満たすときべき級数は収束します。
同様に発散するときも考えます。
$$ \displaystyle \lim_{n \to \infty} \left| \frac{a_{n+1}z^{n+1}}{a_{n}z^n} \right| \gt 1 $$
この式が成立すればいいので、変形をすると、
$$ |z| \gt \displaystyle \lim_{n \to \infty} \frac{|a_{n}|}{|a_{n+1}|} $$
となり、\( z ) がこの範囲を満たすときべき級数は発散します。
ゆえに収束半径は
$$ R= \displaystyle \lim_{n \to \infty} \frac{|a_{n}|}{|a_{n+1}|} $$
となるわけです。

コーシーアダマールの公式
あるべき級数 \(\displaystyle \sum_{n=0}^{\infty}a_{n}z^n\) の収束半径 \( R \) は
\( 1/{\infty}=0 \) 、\( 1/0=\infty \) のもとで
$$ R= \frac{1}{\displaystyle \varlimsup_{n \to \infty } \sqrt[n]{|a_{n}|}} $$
で求められる
こちらをコーシーアダマールの公式といいます。
ここで \( c = \displaystyle \varlimsup_{n \to \infty } c_{n} \) とは上極限といい、収束する極値のうち最大値のものをいいます。詳しい内容はこんど記事にしますm(_ _”m)
こちらはコーシーの収束判定法をもとにして導出することが出来ます。
ただ、導出は結構大変なので今回は省略します<m(__)m>(どっかで書きます)

まとめ
では今回のまとめです。
まず、べき級数とはそれぞれが固有の円をもっていてそれを収束円、その半径を収束半径といいます。
この収束半径には代表的な求め方が2つあり、
・ダランベールの判定法を用いた公式(係数比判定法)
・コーシーアダマールの公式
です。
今回の記事でなんとなくでもイメージをつかめたらうれしいです!(^^)!
ではまた(^^)/~~~