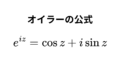こんにちは!
今回はテイラー展開とマクローリン展開について扱っていきます!
関数を式で近似する方法としてとても有名なテイラー展開とマクローリン展開ですが、「結局どう違うの?」「実際どうやって使うの?」と疑問に思っている方も多いと思います^^;
この記事では、まずそれぞれの展開の意味と違いをやさしく解説したあと、具体的な関数を例にとって実際に展開してみます!(^^)!
ではやっていきましょう
テイラー展開とマクローリン展開とは
まずはそれぞれの定義・公式を確認しましょう
テイラー展開の定義
ある関数 \( f(x) \) をある点 \( a \) まわりで展開した式のことをテイラー展開といいます。
公式は以下のとおりです。
$$ f(x) = f(a) + f'(a)(x-a) + \frac{f^{\prime\prime}(a)}{2!}(x-a)^2 + \frac{f^{\prime\prime\prime}(a)}{3!}(x-a)^3 + \cdots $$
もっと一般的に書くと、
$$ f(x) = \displaystyle \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!} (x-a)^n $$
と表すことができます。
このように、関数の値とその導関数を使って、関数を多項式の形で表すことが出来るのです。
マクローリン展開の定義
実はマクローリン展開は、テイラー展開の特別なケースです。
展開する中心の点 \( a \) を \( 0 \) にした場合、それをマクローリン展開といいます。
つまり公式は、
$$ f(x) = f(0) + f'(0)x + \frac{f^{\prime\prime}(0)}{2!}x^2 + \frac{f^{\prime\prime\prime}(0)}{3!}x^3 + \cdots $$
となり、もっと一般的に書くと
$$ f(x) = \displaystyle \sum_{n=0}^{\infty} \frac{f^{(n)}(0)}{n!} x^n $$
となります!
2つの違いは?
2つの違いを簡単にまとめると、
・テイラー展開:任意の点 \( a \) まわりに展開する(より一般的)
・マクローリン展開:\( a=0 \) に限定したテイラー展開
ということになります(*^^)v

いくつかの具体例
それではいくつか代表的な関数についてマクローリン展開・テイラー展開をしてみます!
今回、マクローリン展開はすべて \( a \) まわりで展開するものとします。
例1 \( f(x) = e^x \)
テイラー展開
\( f(x) =e^x \) を微分すると、
\( f'(x)=e^x \) 、 \( f^{\prime\prime}(x)=e^x \) 、 \( f^{\prime\prime\prime}(x) = e^x \) 、、、
となるので、
$$ e^x=e^a + e^a(x-a) + \frac{e^a}{2!}(x-a)^2 + \frac{e^a}{3!}(x-a)^3 + \cdots $$
となります
マクローリン展開
\( a=0 \) のときを考えればいいので、
$$ e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!} + \cdots $$
となります
例2 \( f(x) = \sin x \)
テイラー展開
\( f(x) = \sin x \) を微分すると、
\( f'(x)=\cos x \) 、 \( f^{\prime\prime}(x) = -\sin x \) 、 \( f^{\prime\prime\prime}(x) = -\cos x \) 、、、
となるので、
$$ \sin x =\sin a + \cos a (x-a) – \frac{\sin a}{2!} (x-a)^2 – \frac{\cos a}{3!} (x-a)^3 + \cdots $$
となります
マクローリン展開
\( a=0 \) のときを考えればいいので
$$ \sin x = x – \frac{x^3}{3!} + \frac{x^5}{5!} – \frac{x^7}{7!} + \cdots $$
となります
例3 \( f(x) = \cos x \)
テイラー展開
\( f(x) = \cos x \) を微分すると、
\( f'(x)=- \sin x \) 、 \( f^{\prime\prime}(x) = -\cos x \) 、 \( f^{\prime\prime\prime}(x) = \sin x \) 、、、
となるので、
$$ \cos x =\cos a – \sin a (x-a) – \frac{\cos a}{2!} (x-a)^2 + \frac{\sin a}{3!} (x-a)^3 + \cdots $$
となります
マクローリン展開
\( a=0 \) のときを考えればいいので
$$ \cos x = 1 – \frac{x^2}{2!} + \frac{x^4}{4!} – \frac{x^6}{6!} + \cdots $$
となります
まとめ
いかがだったでしょうか!(^^)!
実はこれら展開を用いることでオイラーの公式を導きだせちゃったりもします(*^^*)
これはまた今度やります
関数を近似する方法として、テイラー展開とマクローリン展開に慣れてくれたらうれしいです!
ではまた(^^)/~~~