こんにちは!
今回は
・多価関数
・リーマン面
この2つについて話していきたいと思います。
ではさっそくやっていきましょう!
多価関数とは?
多価関数とは、
独立変数1つの値に対して、従属変数の値が2つ以上あるような関数
です。
“(-“”-)”。。。?
となる方もいると思うのでわかりやすく説明していきます!
まず、私たちが高校数学で今までやっていた関数というのは、
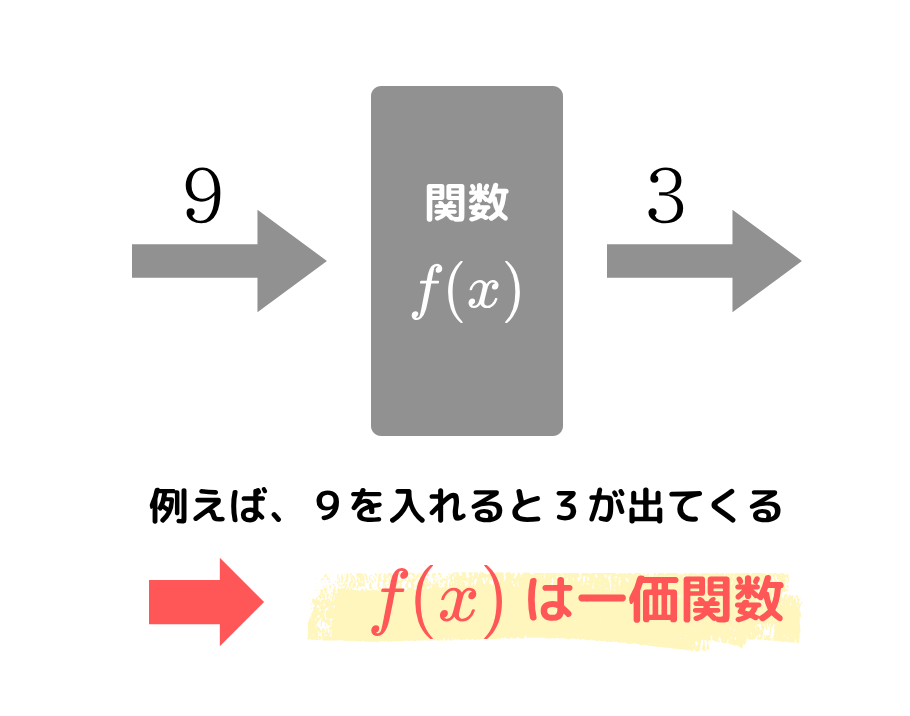
関数 \( y= f(x) \) においてあるひとつの \( x \) の値を入れると \( y \) の値もあるひとつが出てくる
というものでしたね。
このとき \( f(x) \) は一価関数といいます。
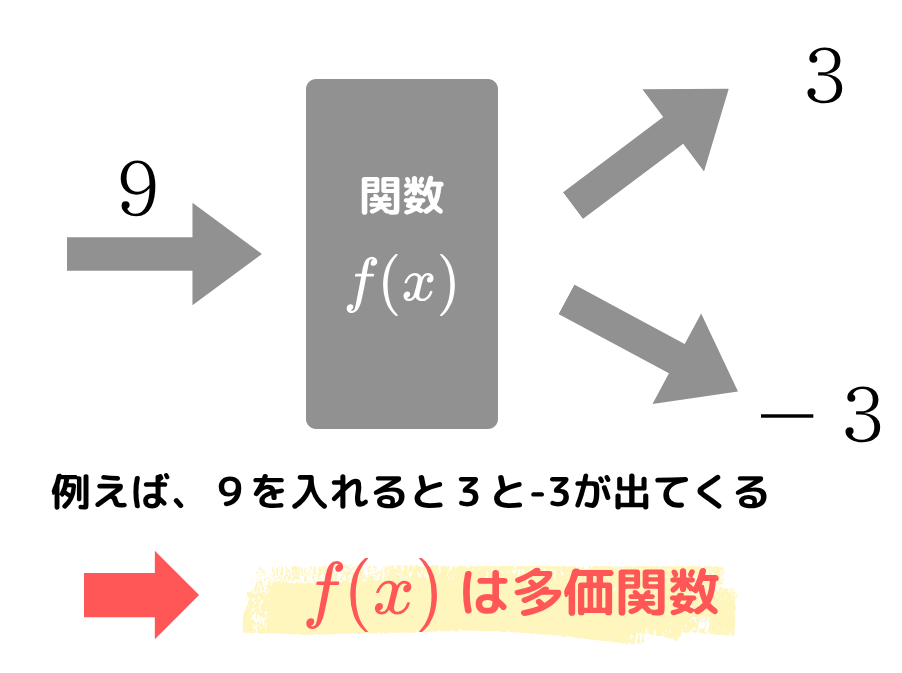
これに対して多価関数とは、あるひとつの\( x \) の値を入れると \( y \) の値が2つ以上出てくるものをいいます!
この内容を踏まえて次にリーマン面について進みたいと思います!
リーマン面とは (ざっくり)
リーマン面とは多価関数を一価関数として扱うための幾何学的な道具です。多価関数を通して出てきた2つ以上の値を複素平面上で切り貼りすることで1つの面を作成し、一価関数のように見ることが出来ます。
そんなこと言われても、なんとなくわかったようなわからないような、、、という気持ちになると思います。
具体的な多価関数を見ながらなるべくわかりやすく説明していきます!
具体的なリーマン面を説明
よく用いられる代表的な多価関数として
$$ \omega = \sqrt{z} $$
があります。
今回はこの関数のリーマン面を考えてみましょう
\( \sqrt{z} \) のとる値を考える
前提知識として複素対数関数 \( \log z \) があったとき、
$$ \log z = \log |z| + i (\arg z +2n \pi ) $$
と、実部と虚部に分けられることを使います。
この式の導出については以下の記事をご覧ください↓↓↓
\( z^{\frac{1}{2}} = e^{\frac{1}{2} \log z} \) と変形することが出来るので、
$$ \begin{eqnarray}
\omega &=& z^{\frac{1}{2}} \\[7pt]
&=& e^{\frac{1}{2} \log z} \\[7pt]
&=& e^{\frac{1}{2} \{ \log r + i(\theta + 2n \pi) \} } \\[7pt]
&=& \sqrt r e^{i(\frac{\theta}{2}+n \pi )} \\[7pt]
\end{eqnarray} $$
となります。
\( n \) を場合分けすることによって、
$$ \begin{eqnarray}
& & \omega_{1} = \sqrt r e^{i \frac{\theta}{2}} \quad (n=2m) \\[7pt]
& & \omega_{2} = \sqrt r e^{i (\frac{\theta}{2} + \pi )} \quad (n=2m+1) \\[7pt]
\end{eqnarray} $$
ここから、 \( \omega \) は多価関数 (2価関数) であることがわかります。
\( \sqrt z \) は \( \theta \) をどのように定義するかによって値が変わってしまうのです。
このままだと何が問題か
\( \omega \) について偏角 \( \theta \) を \( 2 \pi \) まわすと符号が反転してしまいます。
実際、\( \theta = 2 \pi \) を代入すると、
$$ \omega_{1} = \sqrt r e^{i \pi} = \sqrt r (\cos \pi + i \sin \pi ) = -\sqrt r $$
$$ \omega_{2} = \sqrt r e^{i 2 \pi} = \sqrt r (\cos 2 \pi + i \sin 2 \pi ) = \sqrt r $$
と、符号が反転しているのがわかりますね。
これを解決するための発想がリーマン面です。
リーマン面の発想に触れる前に分岐点について説明したいと思います。
分岐点とは
偏角 \( \theta \) が \( 0 \) から \( 2 \pi \) まで変化しているとき、 \( \sqrt z \) は原点まわりをぐるっと一周しています。
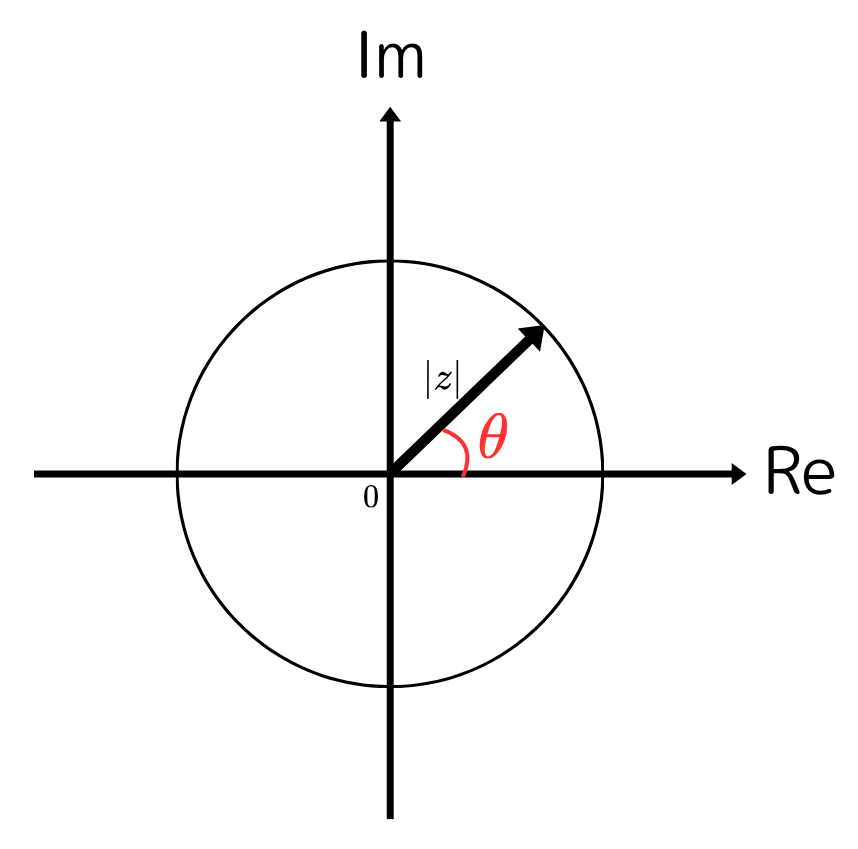
このある点のまわりを一周すると、関数の値が変わってしまうような点を分岐点 (branch point) といいます。
そして図から今回の分岐点は原点であることがわかります。
それではリーマン面の考え方に移っていきましょう!(^^)!
リーマン面の発想
リーマン面では、複素平面を2枚用意し、それぞれ平方根の枝 ( \( \omega_{1} \) と \( \omega_{2} \) ) に割り当てます。
そして分岐点 (原点) を中心に回ると、次のシートに移るようにします。
こうしてひとつの複素平面上で表すわけです。
整理してひとつずつやってみましょう
1. 2枚のシート (複素平面) を準備する
今回のシートは
第1シート : \( \sqrt z = \sqrt r e^{i \frac{\theta}{2}} \)
第2シート : \( \sqrt z = \sqrt r e^{i (\frac{\theta}{2} + \pi )} \)
です。
2. ブランチカット (branch cut)
分岐点 (原点) から負の実軸に沿って切り取りを入れます。
この切り取り線をまたぐと別のシートに移動するというような感じになります。
このように、ブランチカット (branch cut) とは複素平面の切れ目のところで関数を定義しないようにして、ほかの部分では一貫して関数の値を選べるようにするというアイデアです。
これにより関数を無理やり一価関数にすることが出来ます。
3. シートをつなげる
最後に第1シートと第2シートを接着します。
第1シートのブランチカットの上側と、第2シートのブランチカットの下側を繋げます。
逆に、第1シートの下側と第2シートの上側も繋げます。
このようにしてできたリーマン面上では、点 \( z \) を一周すると、最初とは異なる平方根の値になるけれど、次のシート上では連続になります。
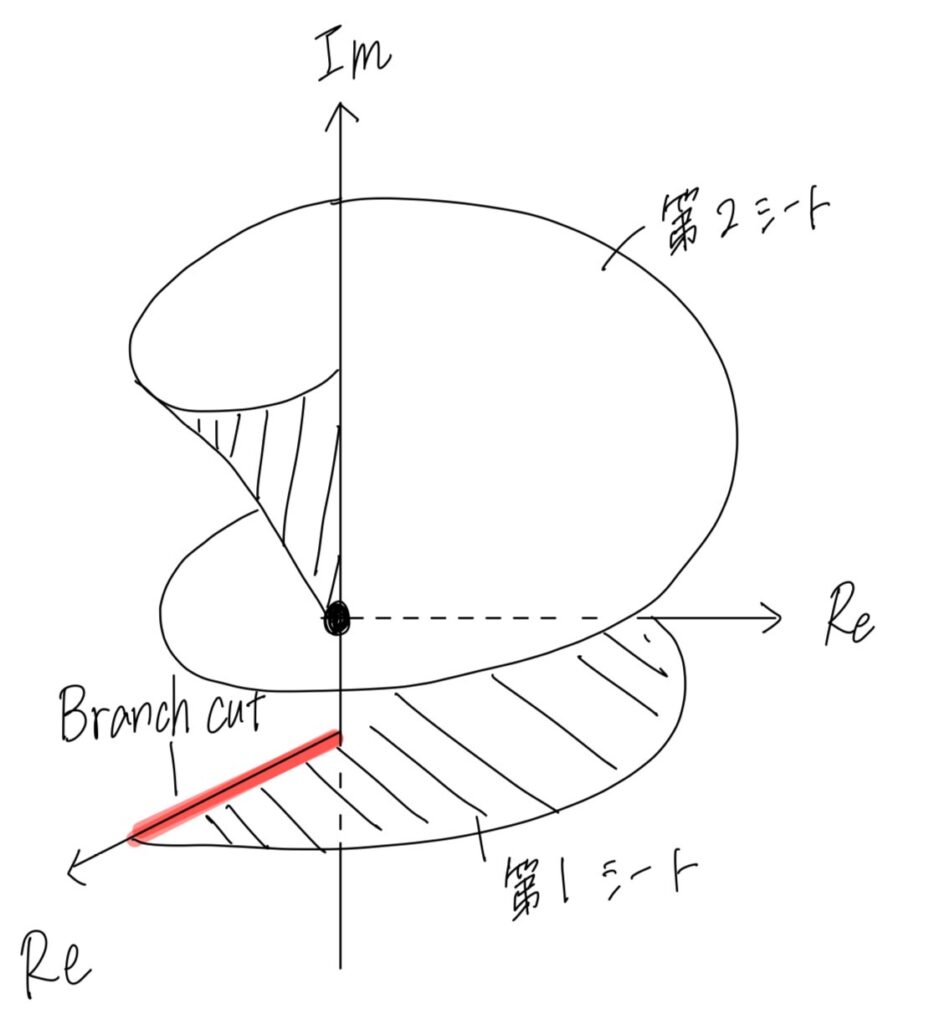
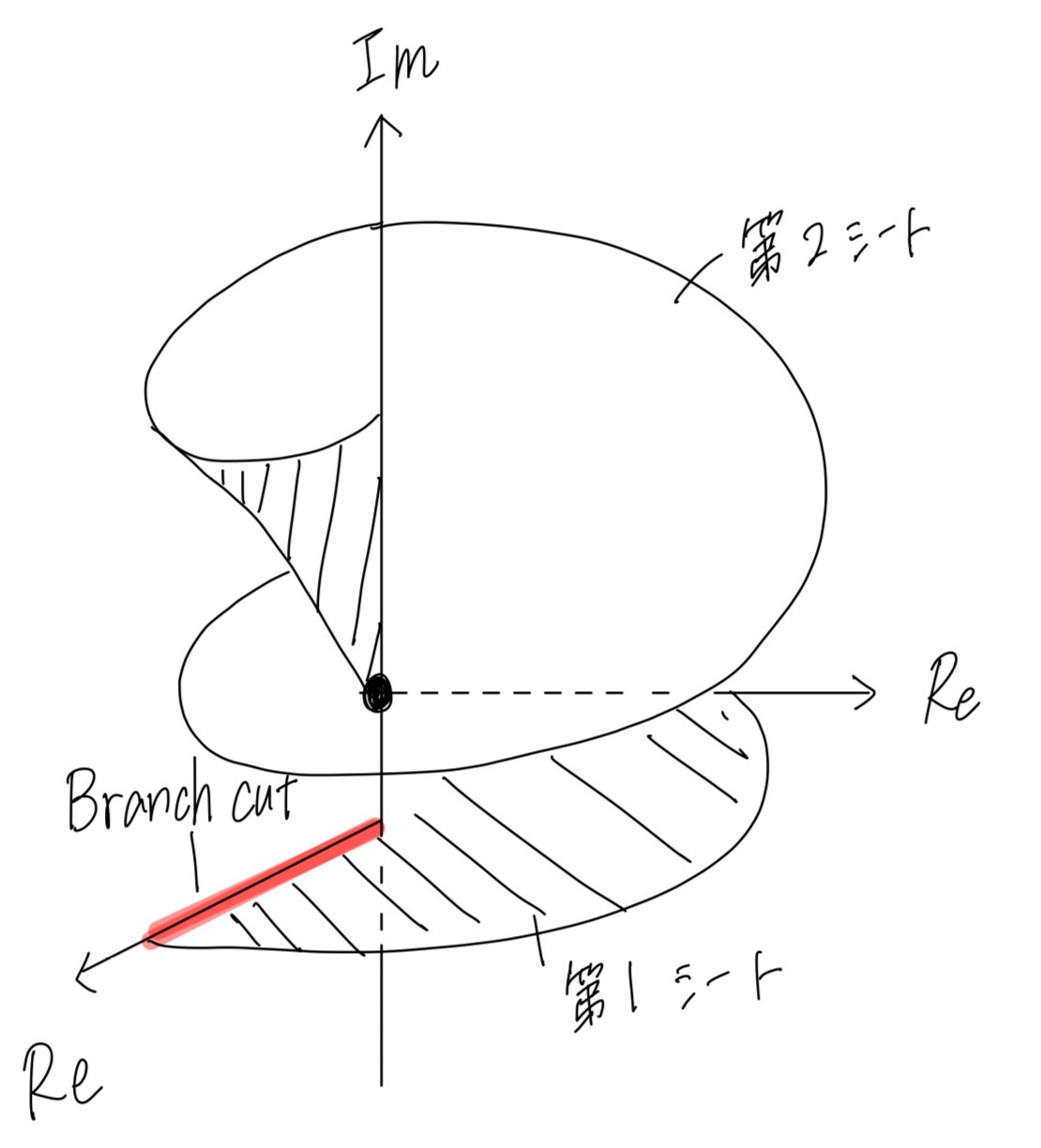
視覚的にとらえられるように頑張って描いてみたのですが、余計ややこしくさせたらすみません”(-“”-)”
リーマン面で画像検索するといろんなのが出てくるので調べてみてください
こんな感じにねじれ構造となっており、第1シートと第2シートはスパイラル状に接続されています。
原点まわりを一周するとシートが入れ替わる感じが(おそらく)見て取れると思います。
まとめ
今回の内容は以上になります!
リーマン面あたりがすごくややこしかったと思います。
なるべくわかりやすく説明したつもりですが、少しでも理解出来たらうれしいです!
ではまた!