こんにちは!
今回は主にエントロピーについて扱っていきます
エントロピーはイメージしずらくどんなものかといわれてもよくわからないと思うので、なるべくわかりやすく解説してみます!(^^)!
エントロピーを導くための準備
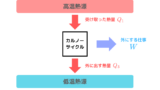
カルノーサイクルでは高温熱源から熱量 \( Q_{1} \) を受け取り、外に仕事 \( W \) をして低温熱源に \( Q_{2} \) の熱量を放出していました。
これらはエネルギー保存則より
$$ Q_{1} = Q_{2}+W $$
となります。
この式からわかるように熱量というものは変化しているわけですから保存されません。
つまり状態量とはいえないわけです。
ここでカルノー機関という系において内部エネルギーのほかに何か保存される量はないかなと考えるわけです。
ここで生まれたのがエントロピーです。
では次は導出に移ります。
エントロピーの導出
まずはカルノーサイクルの熱効率からです。これは前回の記事で書いたため求め方は省略します。
気になる方は以下の記事を読んでみてください↓↓↓
以下のグラフになるようなカルノー機関を考えます。
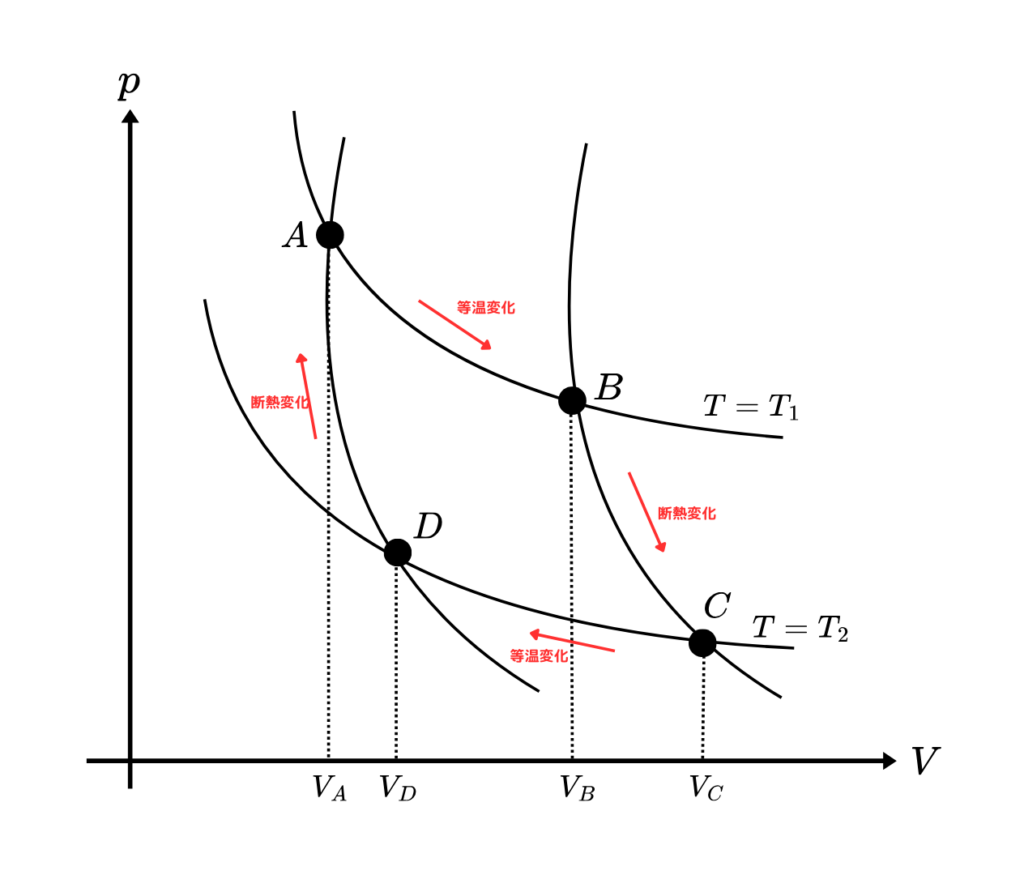
熱効率 \( e \) は
$$ e = 1- \frac{Q_{2}}{Q_{1}} = 1 – \frac{T_{2}}{T_{1}} $$
と表せられます。
これを少し変形すると
$$ \frac{Q_{1}}{T_{1}} = \frac{Q_{2}}{T_{2}} $$
こうなります。
それぞれの辺で熱量を温度で割ったものが等しい値を取っています。
ここでエントロピー \( S \) とは
$$ S = \frac{Q}{T} $$
と表せるのです。
このエントロピーというものは状態量であり、1サイクルにおいて保存される量です。
エントロピーのもっとざっくりとしたイメージ
エントロピーがどういう式で表される状態量なのかは理解できたと思いますがこの式だけ見ても
(+_+)「だからなに?結局なんなの?」
となると思いますのでもっとざっくりとイメージしてもらいたいと思います。
エントロピーというのは原子・分子の乱雑さをあらわしています。
下の図を見てみてください
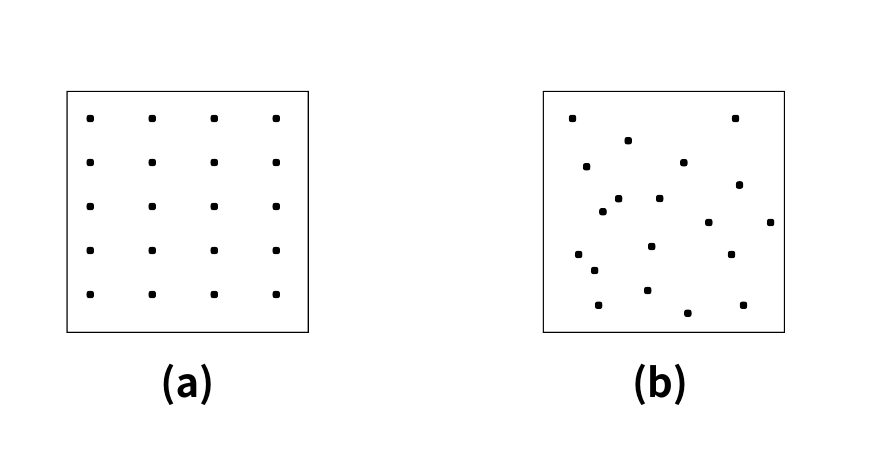
それぞれ2つの容器(a)、(b)があり、中には分子が入っています。
エントロピーというのは乱雑さを表す状態量なので容器(b)のほうが(a)よりもエントロピーが大きい、と視覚的にとらえることができるのです!(^^)!

カルノーサイクルのエンタルピーとTS図
では先ほどのカルノー機関

の熱量、仕事をエントロピーを使って考えていきましょう
エントロピーの微小量 \( dS \) は
$$ dS = \frac{\delta Q}{T} $$
となります。
断熱変化 B→C 、D→A については熱の出入りがないため \( \delta Q = 0 \) です。
したがって \( dS = 0 \) となりエントロピーは変化しません。
次に等温変化のときです。まず A→B のときの熱量は
$$ \begin{eqnarray}
Q_{1} &=& \int_{A}^{B} T_{1} dS \\[7 pt]
&=& T_{1}(S_{B}-S_{A}) \\[7pt]
\end{eqnarray} $$
となります。
同様に考えると C→D のときは
$$ Q_{2} = T_{2}(S_{B}-S_{A}) $$
となります。
この時の仕事は
$$ \begin{eqnarray}
W &=& Q_{1}-Q_{2} \\[7 pt]
&=& T_{1}(S_{1}-S_{2}) – T_{2}(S_{1}-S_{2}) \\[7pt]
&=& (T_{1}-T_{2})(S_{1}-S_{2}) \\[7pt]
\end{eqnarray} $$
となります。
これのTS図を考えてみましょう。横軸がエントロピー \( S \)、縦軸が温度 \( T \) です。
断熱過程のときはエントロピー \( S \) が一定で等温過程のときは温度 \( T \) が一定です。
このことをふまえると、
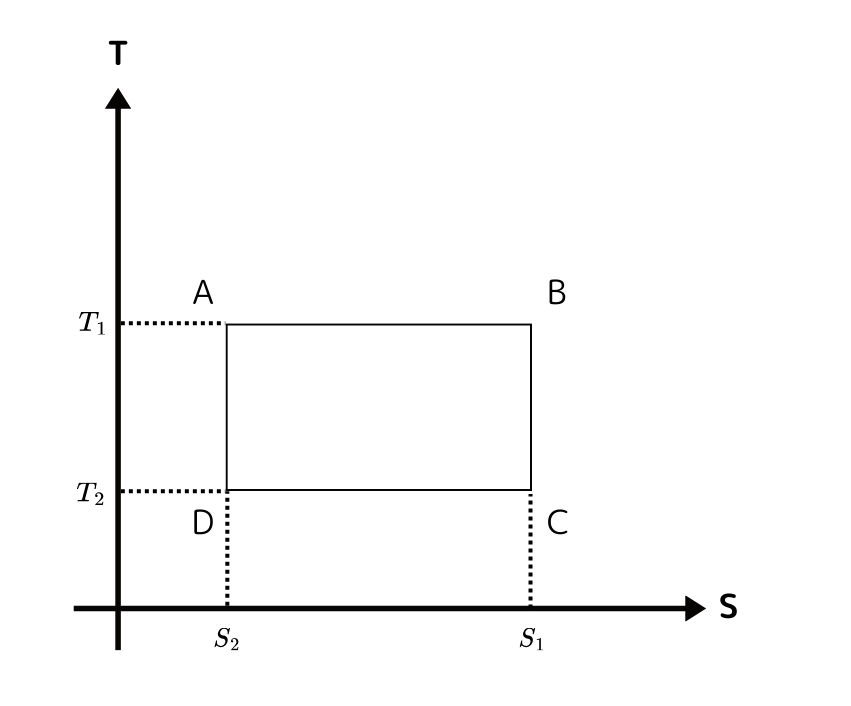
このようになります(*^^)v
先ほど求めた熱量と仕事を照らし合わせてみると
熱量 \( Q_{1} \) は A から B までの体積を表しており、 \( Q_{2} \) も同様のことが言えます。
また、仕事については1サイクルでできた長方形の体積に相当していることがわかります。
まとめ
いかがだったでしょうか!(^^)!
すこしでもエントロピーについてイメージしやすくなっていたらうれしいです
ではまた(^^)/~~~