こんにちは!
今日は内部エネルギーのイメージを図を使って説明してみます。
さっそくやっていきましょう
内部エネルギーってなに?
ここにある容器があるとします。
容器の外から力学的仕事を加えると、容器内の温度は上昇します。
同様にその容器の外から熱量を加えると、容器内の温度は上昇します。

この時、容器内に入ってしまった熱量や仕事はその容器内で区別することが出来ませんね。
つまり熱や仕事はその系をあらわす状態量にはなりえないといえます。
そして容器内にを粒子による運動エネルギーや位置エネルギーなるものが存在します。
これら容器内の全エネルギーをあらわしたものを内部エネルギーと呼びます。
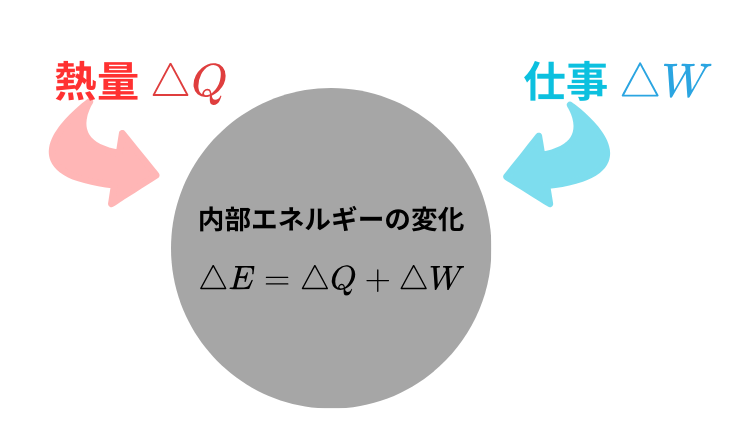
もし熱量 \( \Delta Q \) 、仕事 \( \Delta W \) を容器内に加えたときの内部エネルギーの変化 \( \Delta E \) は、
$$ \Delta E = \Delta Q + \Delta W $$
と表せられます。
エネルギーの保存と変化
内部エネルギーが変化するためには外から仕事や熱を加えなければなりません。
つまり外から何も加えなければ内部エネルギーはずっと変化しないままなのです!
これを熱力学第1法則といいます。
また、エネルギーの変化は途中過程によりません。
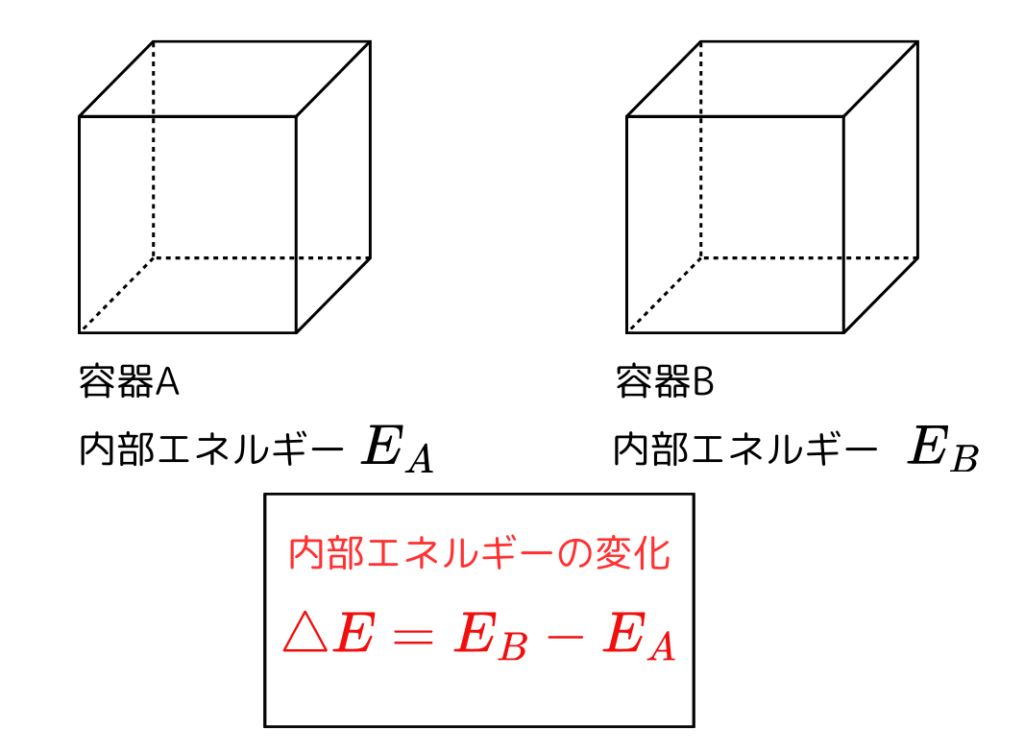
例えば熱や仕事を加えことで内部エネルギーが \( E_{A} \) から \( E_{B} \) に変化したときを考えます。
この時の内部エネルギーの変化は
$$ \Delta E = E_{B} – E_{A} $$
です。
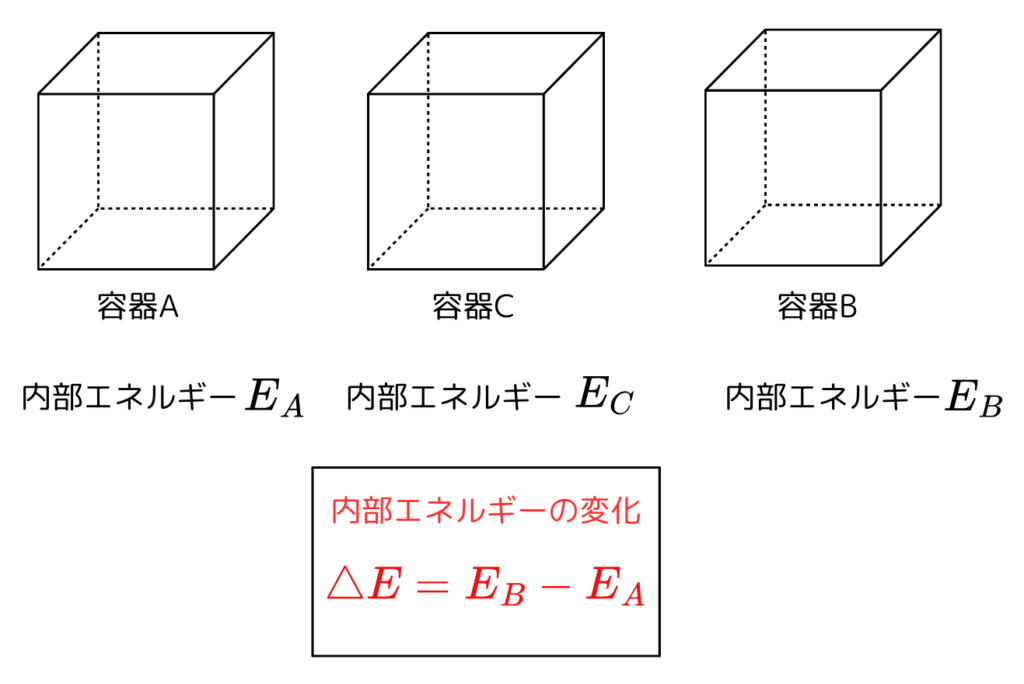
次に容器内の内部エネルギーが \( E_{A}\) から \( E_{C} \) を通って \( E_{B} \) に変化した時を考えます。
\( E_{A} \) から \( E_{C} \) までの内部エネルギーの変化は\( E_{C} – E_{A} \) です。
同様に \( E_{C} \) から \( E_{B} \) までの内部エネルギーの変化は \( E_{B} – E_{C} \) です。
これより全体の変化は
$$ \Delta E = ( E_{C} – E_{A} ) + ( E_{B} – E_{C} ) $$
となり、
$$ \Delta E = E_{B} – E_{A} $$
となります。
結局内部エネルギーの変化量は同じ値になりました。
このように内部エネルギーの変化は途中過程によらず最初と最後の値のみに依存するのです。
熱機関
では熱や仕事を系に加えたとき、最終的に内部エネルギーが最初のときと同じ値になることを考えます。
つまり、
$$ \Delta E = 0 $$
です。
このように再び元の状態に戻ることを循環過程(サイクル)と呼びます。
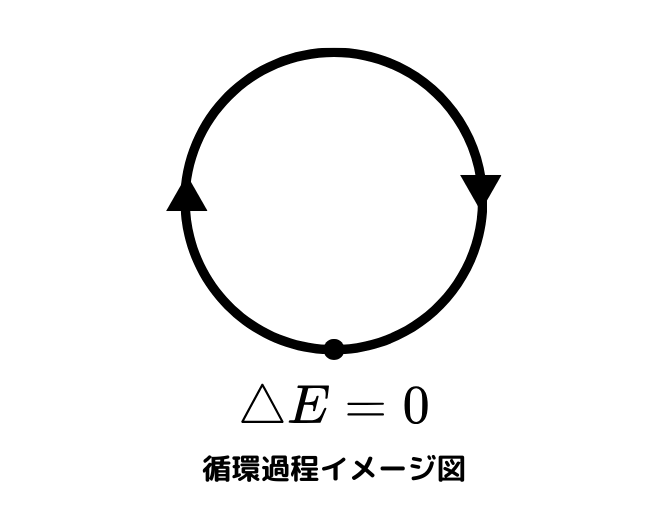
このような循環過程をする機械を熱機関といいます。
\( \Delta E = 0 \) であるということは
$$ \Delta Q + \Delta W = 0 $$
ということです。つまり
$$ \Delta Q = – \Delta W $$
となるので、このことから
熱機関が外に仕事をする分 \( -\Delta W \) の熱量を外から加えなければならない \( \Delta Q \) ことがわかります。
熱量以上の仕事を外にする機関を第一種永久機関といいますが、これは現実的に考えてあり得ないこともこの式からわかりました。
まとめ
いかがでしたか(o^―^o)
第一種永久機関が発明されたらうれしいですね!!!!
ではまた!


