こんにちは!
無限級数が絶対収束するかどうかの判定方法には
・コーシーの積分判定法
があります。
今回はその中でコーシーの積分判定法をやっていきたいと思います。
絶対収束ってなに?という方はこちらをまずご覧ください↓↓↓
ではやっていきましょう!
コーシーの積分判定法
無限級数 \( \displaystyle \sum_{n=1}^{\infty} a_{n} \) があったとき、その正項級数 \( \displaystyle \sum_{n=1}^{\infty} |a_{n}| \) の収束性は
\( |a_{n}|=f(x) \) を満たす0以上の単調減少関数 \( f(x) \) があるとき、
① \( \int_{1}^{\infty} f(x) dx \) が収束ならば級数は絶対収束
② \( \int_{1}^{\infty} f(x) dx \) が発散ならば級数は発散
となります。

コーシーの積分判定法の証明
それではコーシーの積分判定法を証明してみましょう。
\( f(x) \) を \( f(n) = |a_{n}| \) となる正の単調関数であるとします。
ここで、\( \displaystyle \sum_{n=1}^{\infty} a_{n} \) と \( \int_{1}^{\infty} f(x) dx \) の大小関係を比較します。
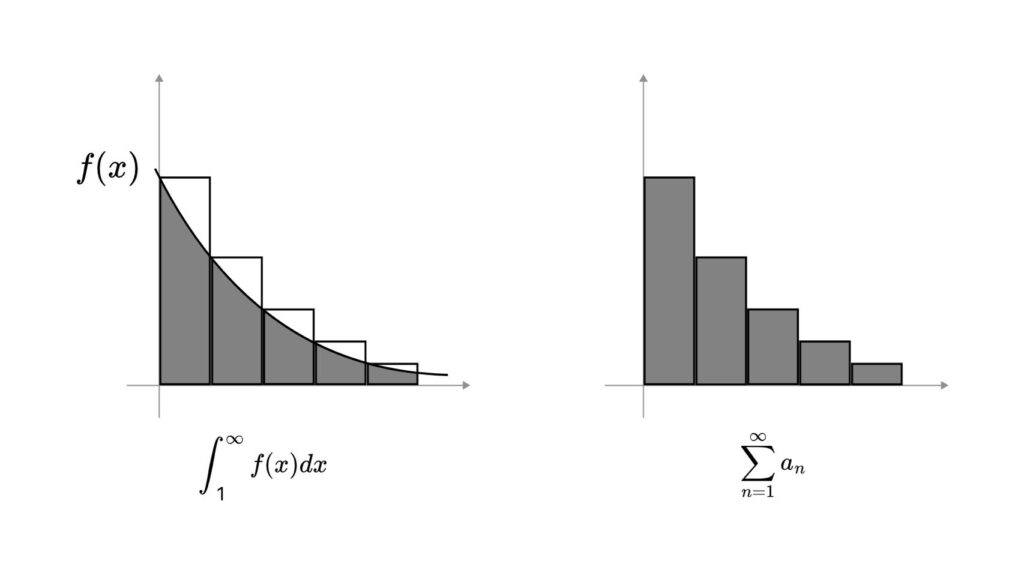
この図から \(\int_{1}^{\infty} f(x) dx \lt \displaystyle \sum_{n=1}^{\infty} a_{n} \) であることがわかります。
また図からわかる通り、 \( \displaystyle \sum_{n=1}^{\infty} a_{n} \lt \int_{1}^{\infty} f(x) dx + a_{1} \) でもあるので、これらをまとめると
$$ \int_{1}^{\infty} f(x) dx \lt \displaystyle \sum_{n=1}^{\infty} a_{n}\lt \int_{1}^{\infty} f(x) dx + a_{1} $$
という大小関係がわかります。
これより、 \( \int_{1}^{\infty} f(x) dx \) が発散する場合、\( \sum_{n=1}^{\infty} a_{n} \) も発散することがわかります。
また、 \( \int_{1}^{\infty} f(x) dx \) に有限値がある場合は、\( \sum_{n=1}^{\infty} a_{n} \) は \( \int_{1}^{\infty} f(x) dx \) と \( \int_{1}^{\infty} f(x) dx + a_{1} \) の間に収束することがわかります。
これにて証明ができました!(^^)!
コーシーの積分判定法の具体例
では具体的に問題を解いていきましょう。
今回は \( p \) 級数について扱ってみます。
無限級数
$$ \displaystyle \sum_{n=1}^{\infty} \frac{1}{n^p} \qquad (p \gt 0 ) $$
が絶対収束するか確かめよ
[解き方]
まず、 \( f(x) = \frac{1}{x^p} \) を考えます。これは単調増加です。
\( p \neq 1 \) のとき
$$ \begin{eqnarray}
& & \int_{1}^{\infty} \frac{1}{x^p} dx \\[7pt]
&=& \displaystyle \lim_{t \to \infty} \int_{1}^{t} x^{-p} dx \\[7pt]
&=& \displaystyle \lim_{t \to \infty} \left[ \frac{x^{-p+1}}{-p+1} \right]_{1}^{t} \\[7pt]
&=& \displaystyle \lim_{t \to \infty} \frac{t^{-p+1}-1}{-p+1} \\[7pt]
\end{eqnarray} $$
これを \( p \) で場合分けします。
(1) \( p \gt 1 \) のとき
$$ \displaystyle \lim_{t \to \infty} \frac{t^{-p+1}-1}{-p+1}=0 $$
より収束
(2) \( 0 \lt p \lt 1 \) のとき、
$$ \displaystyle \lim_{t \to \infty} \frac{t^{-p+1}-1}{-p+1} = \infty $$
より発散
(3) \( p=1 \) のとき
$$ \begin{eqnarray}
& & \int_{1}^{\infty} \frac{1}{x} dx \\[7pt]
&=& \displaystyle \lim_{t \to \infty} \log t
&=& \infty \\[7pt]
\end{eqnarray} $$
より発散
(1)から(3)をまとめると、
\( p \gt 1 \) のとき無限級数は絶対収束
\( 0 \lt p \leqq 1 \) のとき無限級数は発散
と求めることが出来ました!
まとめ
いかがだったでしょうか!
コーシーの積分判定法をつかって絶対収束を調べられるようになれたらうれしいです!!
ではまた(^^)/~~~