こんにちは!
今回は大学で扱う熱力学のまず初めの部分を扱います。
今回の内容がこれからの熱力学の基礎となるものなのでしっかり理解しておきましょう。
熱容量と比熱
熱というのは熱いものから冷たいものへ移動していきます。
このエネルギーの流れを量的に表したものが熱量です。
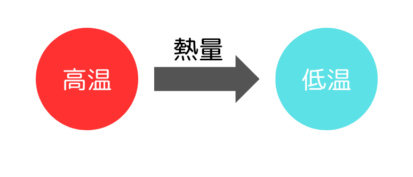
熱量はこのように温度の変化により生じるともいえます。
これを式で表すと
$$ Q=C \Delta T $$
となります。 \( Q \) は熱量[J]、\( \Delta T \) は温度変化[K]です。
そしてこの比例係数 \( C \) を熱容量[J/K]といいます。
熱容量とは物体の温度を 1 [K] 上げるために必要な熱量のことです。
ここでもし物体の質量を2倍にすると、物体を 1 [K] 上げるのに必要な熱量も2倍になりますね。
つまり熱容量とは質量に比例するのです。
$$ C = mc $$
です。 \( m \) は物体の質量[g]です。
そしてこの比例係数 \( c \) を比熱[J/(g・K)]といいます。
ここからわかるように比熱とは1[g]の物体の温度を1[K]上げるために必要な熱量を表します。

そして比熱とは物体によってそれぞれ固有の値があります。
潜熱とは?
物体が気体、液体、固体の状態を熱力学ではそれぞれ気相、液相、固相とよびます。
そして物体の相の変化を相転移とよびます。
基本的に温度によって物体の相は変化していきます。
仮に氷を加熱していった時の温度変化をグラフにしてみます。
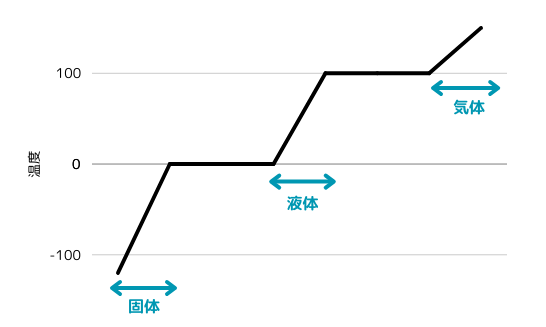
このグラフを見てみると温度が一定のところは相転移をおこしています。
つまりそれぞれ固体と液体が混ざった状態、液体と気体が混ざった状態です。
物体を加熱しているわけですから温度は一定であっても熱量は発生しているわけです。
そしてこの熱量は物体の状態変化に使われています。
この温度が一定のもとで相が変化する際に吸収したり放出したりする熱量のことを潜熱といいます。
融解熱、凝固熱、気化熱などです。
示量性状態量と示強性状態量
次に示量性状態量と示強性状態量の違いについてです。
ある容器があったとして、その容器とその容器の2倍のサイズを考えてみます。
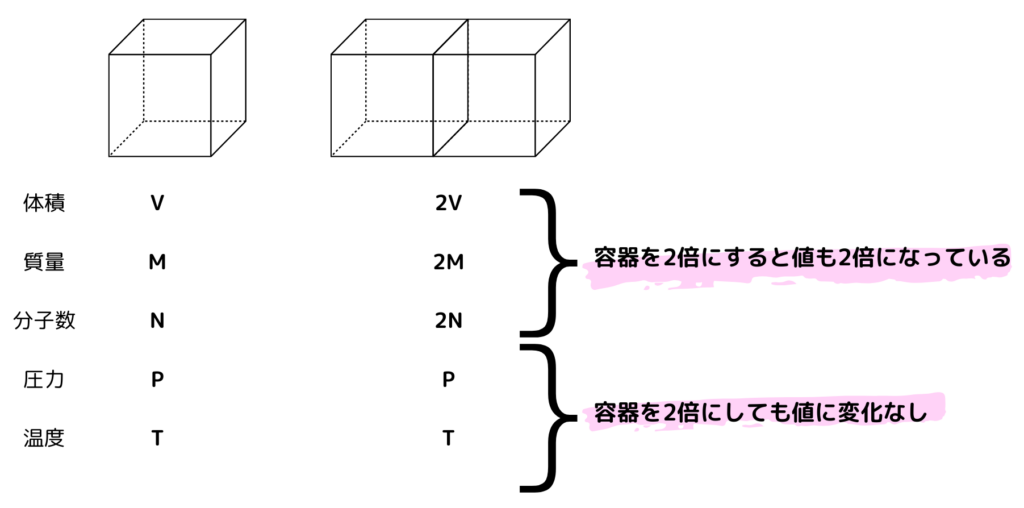
この図からわかる通りこの系の大きさに比例するものと変化しないものがあります。
このうち系の大きさに比例するものを示量性状態量
そして変化しないものを示強性状態量といいます。

状態方程式
知ってる方が多いかもしれませんが、体積 \( V \) の中に閉じ込められた圧力 \( p \) , 温度 \( T \) の理想気体の間には
$$ pV=nRT $$
という関係性が成立します。
この式を理想気体の状態方程式と呼びます。
実際には分子の間に働く力や分子自身の体積などの影響があるためあくまで理想気体でのはなしですが。(ちなみにもう少し現実的な式としてファンデルワールスの状態方程式というものがあります。)
状態方程式は \( T , p , V \) の間で成立しているので
$$ f(T,p,V) = 0 $$
と表したりします。
この方程式をたとえば \( p \) について解いてみると、
$$ p=p(T,V) $$
となります。
左辺は状態量 \( p \) ,右辺は \( T \) と \( V \) の関数を意味しています。
同様にして \( V \) 、\( T \) についても解いてみると
$$ V = V(p,T) $$
$$ T = T(p,V) $$
となります。
まとめ
今回扱った熱力学の基礎知識はこれから大事なのでかならず押さえておきましょう!
ではまた(o^―^o)