こんにちは!
今日はマイヤーの法則とルニョーの法則を導出します。
自分なりになるべくわかりやすくまとめてたのでぜひ読んでください!
準備
まずは準備段階です。
熱力学第1法則から
$$ \delta Q = dE + pdV \quad \cdots (1) $$
があります。これがひとつめの式です。(ちなみに状態量であるものは \( d \) 、そうでないものは \( \delta \) で表して使い分けています。)
次に内部エネルギー \( E \) を \( T \) と \( V \) の関数とみます。(理想気体の状態方程式から \( T , V \) が決まれば自動的に \( p \) も決まります。)
$$ E = E(T,V) $$
と表せられますね。
これを全微分します。
$$ dE = \left(\frac{ \partial E}{ \partial T} \right)_{V}dT + \left(\frac{ \partial E}{ \partial V} \right)_{T}dV \quad \cdots(2) $$
ちなみにですが、たとえば \( \left(\frac{ \partial E}{ \partial T} \right)_{V} \) は体積を一定に保ったまま内部エネルギーを温度で微分する、という意味です。
(2)式を(1)式に代入すると
$$ \delta Q = \left(\frac{ \partial E}{ \partial T} \right)_{V}dT + \left(\frac{ \partial E}{ \partial V} \right)_{T}dV + pdV $$
整理すると、
$$ \delta Q = \left(\frac{ \partial E}{ \partial T} \right)_{V}dT + \{ p+ \left(\frac{ \partial E}{ \partial V} \right)_{T} \} dV \quad \cdots(3) $$
が誕生します。
ここまでが準備段階です。
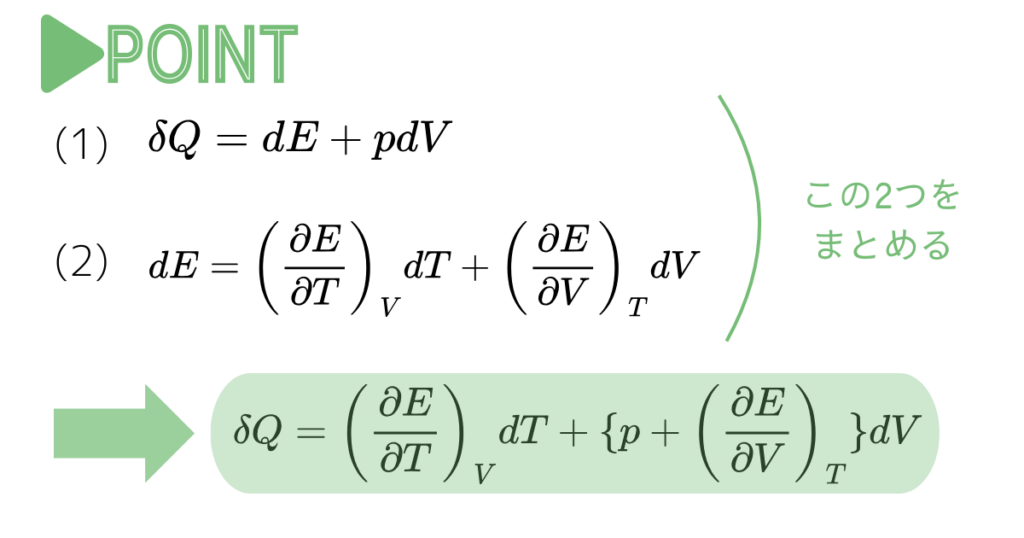
定積熱容量
定積熱容量 \( C_{V} \) とは名前の通り物体の体積を一定に保ったまま温度を1K上げるために必要な熱量のことです。
式で表すと
$$ C_{V} = \frac{ \delta Q}{dT} \quad \cdots(4) $$
となります。
また、体積が一定なので \( dV = 0 \) です。これより先ほど作った(3)式の第2項は消えます。
よってこれと(4)式から
$$ C_{V} = \left( \frac{ \partial E}{ \partial T} \right)_{V} \quad \cdots (5) $$
と、\( C_{V} \) を表すことが出来ました!

定圧熱容量
定圧熱容量 \( C_{p} \) とは名前の通り物体の圧力を一定に保ったまま温度を1K上げるために必要な熱量のことです。
式で表すと
$$ C_{p} = \frac{ \delta Q}{dT} \quad \cdots(6) $$
となります。
また、体積 \( V \) を \( T , p \) の関数とみると
$$ V = V(T,p) $$
となります。
これを全微分すると
$$ dV = \left ( \frac{ \partial V}{ \partial T} \right )_{p}dT + \left ( \frac{ \partial V}{ \partial p} \right ) _{T}dp \quad \cdots(7) $$
となります。
(7)式を(3)式に代入すると
$$ \delta Q = \left(\frac{ \partial E}{ \partial T} \right)_{V}dT + \left \{ p+ \left(\frac{ \partial E}{ \partial V} \right)_{T} \right \} \left \{ \left ( \frac{ \partial V}{ \partial T} \right )_{p}dT + \left ( \frac{ \partial V}{ \partial p} \right ) _{T}dp \right \} $$
(5)式を用いて整理すると、
$$ \delta Q = \left [ C_{V} + \left \{ p+ \left ( \frac{ \partial E}{ \partial V} \right )_{T} \right \} \left ( \frac{ \partial V}{ \partial T} \right )_{p} \right ]dT + \left \{ p+ \left ( \frac{ \partial E}{ \partial V} \right )_{T} \right \} \left ( \frac{ \partial V}{ \partial p} \right )_{T}dp $$
圧力が一定なので \( dp= 0 \) より第2項が消えて、
$$ \delta Q = \left [ C_{V} + \left \{ p+ \left ( \frac{ \partial E}{ \partial V} \right )_{T} \right \} \left ( \frac{ \partial V}{ \partial T} \right )_{p} \right ]dT $$
(6)式から
$$ C_{p} – C_{V} = \left \{ p+ \left ( \frac{ \partial E}{ \partial V} \right )_{T} \right \} \left( \frac{ \partial V}{ \partial T} \right )_{p} \quad \cdots (8)$$
となります!

マイヤーの関係式の導出
理想気体に関するジュールの法則は
$$ \left ( \frac{ \partial E}{ \partial V} \right )_{T} = 0 \quad \cdots(9) $$
と表すことが出来ます。
温度一定で気体の体積が変化しても内部エネルギーは変化しないという意味の式です。
これを(8)式に代入すると
$$ C_{p}-C_{V} = p \left ( \frac{ \partial V}{ \partial T} \right )_{p} \quad \cdots(10) $$
理想気体の状態方程式は
$$ pV = nRT $$
なのでこれを \( p \) を一定の状態で両辺 \( T \) で微分すると
$$ p\left ( \frac{ \partial V}{ \partial T} \right )_{p} = nR $$
となります。これを(10)式に代入すると
$$ C_{p}-C_{V} = nR $$
これでマイヤーの関係式が求まりました!

ルニョーの法則の導出
(2)式に(5)式と(9)式を代入すると
$$ dE = C_{V}dT $$
となります。
この式をルニョーの法則といいます。
理想気体の定積熱容量は温度によらず定数であるということがわかります。

まとめ
いかがでしたか(o^―^o)
マイヤーの関係とルニョーの法則を覚えるだけでなく理解もできたらうれしいです!
ではまた!