こんちは(o^―^o)
今回はベルヌーイ型の微分方程式の解き方について扱っていきます。
ではさっそくやっていきましょう。
ベルヌーイ型ってどんなもの?
ベルヌーイ型の微分方程式とは以下のようなものです!
$$ y'(x) + p(x)y(x) + q(x)\{ y(x) \}^n = 0 $$
いままで扱っていた一階の微分方程式に \( \{ y(x) \}^n \) の項がついたかたちです!
まずはこのかたちがベルヌーイ型であることを頭に入れちゃいましょう!
そうしたら次は一般的な解き方をマスターするだけです。
では次は具体的な解き方に進んでいきます。
具体的な解き方!
ベルヌーイ型の微分方程式
$$ \frac{dy(x)}{dx} + p(x)y(x) + q(x)\{ y(x) \}^n = 0 $$
があるとき、
\( u(x) = \{ y(x) \}^{1-n} \)
とおく!!!!!!!
これが今回いちばん大切なことです。
これを \( x \) で微分してみましょう。
$$ \frac{du(x)}{dx} = (1-n)\{ y(x) \}^{-n} \cdot \frac{dy(x)}{dx} $$
となります。この式を変形すると、
$$ \frac{dy(x)}{dx} = \frac{\{ y(x) \}^n}{1-n} \cdot \frac{du(x)}{dx} $$
となります。
これをベルヌーイ型の微分方程式の第一項に代入してみると
$$ \frac{\{ y(x) \}^n}{1-n} \cdot \frac{du(x)}{dx} + p(x)y(x) + q(x)\{ y(x) \}^n = 0 $$
両辺を \( \frac{\{ y(x) \}^n}{1-n} \) でわると、
$$ \frac{du(x)}{dx} + \frac{1-n}{\{ y(x) \}^{n-1}}p(x) + (1-n)q(x) = 0 $$
第2項を \( u(x) = \{ y(x) \}^{1-n} \) でおきかえて、
$$ \frac{du(x)}{dx} + (1-n)p(x)u(x) + (1-n)q(x) = 0 $$
となります。
これは \( u(x) \) に対する線形1階常微分方程式ですね!!!
ここからはいつもの通り解けばOKです。
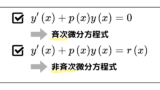
線形1階常微分方程式の解き方が知りたい人はこちらをどうぞ↓↓↓
まとめ
いかがだったでしょうか(^▽^)/
今回のポイントです。
ベルヌーイ型の微分方程式
$$ y'(x) + p(x)y(x) + q(x)\{ y(x) \}^n = 0 $$
があったら、
$$ y=u^{1-n} $$
とおき、\( u \) に対する線形1階常微分方程式に変換する。
こちらをかならず押さえておきましょう!
次回はリッカチ型微分方程式について扱っていきます(o^―^o)
ではまた(^^)/~~~